Quantum Machine Learning Algorithms

Implementing Quantum Kernels & Quantum Neural Networks

What is Quantum Machine Learning?

Quantum Machine Learning (QML) is an interdisciplinary field that applies quantum computing to traditional machine learning tasks. But, classical machine learning already does that, so quantum machine learning algorithms must propose advantages over their classical counterparts:

The basic unit of information, the qubit, is not a 0 or a 1, but a complex number; depending on several factors, a complex number is minimally several bytes, each of which is eight 0s and
Entanglement exponentially increases the number of complex numbers required to describe a system, which means exponential compression of classical data
Quantum computation is not sequential like classical computation; it is inherently parallel, which allows multiple solutions to effectively be discovered simultaneously
Theoretical research supports the possibility of achieving significant computational speedups over known classical approaches
Data can be mapped not only from classical sources but also from quantum sources such as the proposed Quantum Random Access Memory (QRAM)
Interference can be leveraged to not only increase the probabilities of receiving correct solutions, but also to potentially provide speedups over classical algorithms

Quantum Advantage in Machine Learning

The term “quantum advantage” typically refers to speed, but the term is not strictly defined. When a claim is made that a computation can be performed in 200 seconds that would take a supercomputer thousands of years, that’s a claim of quantum advantage. But, that suggests that there’s only one classification of quantum advantage when, in fact, there are multiple potential advantages:

The “holy grail” of quantum computing is to solve problems that consume considerable time and significant classical resources.
Many hard problems can only be approximated classically, whereas quantum algorithms can offer precise solutions.
Quantum algorithms may solve problems in fewer timesteps than classical algorithms, indicating greater efficiency.
Large datasets that require prohibitive amounts of classical memory may be mapped to a relatively small number of qubits.
As an extension of data compression, quantum computers are a natural fit for finding patterns and relationships in high-dimensional data.
Quantum computers can naturally sample probability distributions for a wide range of applications, including generative algorithms.
Constructive and destructive interference can be leveraged to increase the probability of finding correct solutions and decrease the probability of incorrect solutions.

It’s important to note that quantum algorithms are not guaranteed to be advantageous in any way. Nor can they be expected to realize all of the advantages above. However, the potential to realize these advantages exists, and some quantum machine learning solutions might prove to be exceptionally advantageous.

Quantum Machine Learning Applications

Quantum machine learning (QML) use cases overlap two other major classifications of quantum computing applications: quantum simulation and quantum optimization. Near-term solutions for both incorporate hybrid classical-quantum algorithms that utilize classical neural networks. And anywhere you find a classical neural network, is a potential application of quantum machine learning, as well:

Molecular simulation, the original application of quantum computing, with use cases in drug discovery, material development, and climate modeling
Optimization problems, with particular interest in financial applications, but with broad applicability across many industries, especially those with supply chains
Natural language processing, including the quick and accurate interpretation, translation, and generation of spoken languages
Imaging, including the classification and identification of objects in pictures and videos, and with applications ranging from health care to surveillance to autonomous vehicles
Machine Learning model training, optimizing how artificial neural networks train on classical data to solve the problems above

Quantum Kernels: Concept and Role in Classical Machine Learning

Quantum kernels represent a significant advancement in the intersection of quantum computing and machine learning, offering potential enhancements to classical algorithms. This discussion explores their conceptual foundation, operational mechanics, and the implications for improving classical machine learning efficiency.

Concept of Quantum Kernels

At its core, a quantum kernel is a mathematical function that measures the similarity between data points in a high-dimensional feature space, leveraging the principles of quantum mechanics. The quantum kernel method maps classical data into a quantum feature space using quantum states, which allows for the exploitation of quantum phenomena such as superposition and entanglement. This mapping facilitates more complex representations of data compared to traditional methods, which often rely on linear transformations or polynomial expansions .

Mathematically, the quantum kernel K can be expressed as:

Kij=∣⟨ϕ(xi)∣ϕ(xj)⟩∣^2

where ϕ(x) denotes the quantum feature map applied to classical input vectors . This formulation allows for the computation of a kernel matrix that can be used in various classical machine learning algorithms like Support Vector Machines (SVMs) and clustering techniques .

Role in Enhancing Classical Machine Learning Algorithms

Quantum kernels enhance classical machine learning algorithms by providing several advantages:

Exponential Speedup: Quantum kernel methods have been shown to provide exponential speedup over classical counterparts for specific classification problems. For instance, certain datasets that appear as random noise to classical algorithms can reveal intrinsic patterns when processed by quantum algorithms .

Higher Dimensional Feature Spaces: By mapping data into higher-dimensional spaces, quantum kernels allow for more sophisticated decision This capability is crucial for handling complex datasets where relationships between data points are non-linear .
Improved Classification Performance: Studies have indicated that quantum kernel methods can achieve classification performance comparable to or even exceeding that of classical methods under certain conditions. For example, experiments demonstrated that quantum kernels outperformed classical SVMs in specific tasks involving neuron morphology classification .
Integration with Classical Frameworks: Quantum kernels can be seamlessly integrated into existing classical machine learning frameworks. This compatibility enables researchers to leverage quantum advantages without completely overhauling their current methodologies .

Practical Implementations and Future Directions

The implementation of quantum kernels is facilitated by frameworks such as Qiskit, which provides tools for defining and utilizing quantum kernels within machine learning application]. As research progresses, the focus will likely shift towards optimizing hyperparameters specific to quantum models, further enhancing their efficiency and effectiveness in real-world applications.

In conclusion, quantum kernels represent a promising frontier in machine learning, combining the power of quantum computing with established classical techniques. Their ability to process complex datasets more efficiently than traditional methods could lead to breakthroughs across various domains, including technology, healthcare, and finance. As advancements continue, the potential for quantum kernels to revolutionize machine learning remains significant.

Principles of Quantum Neural Networks (QNNs)

Quantum Neural Networks (QNNs) represent an innovative fusion of quantum computing principles and neural network architectures, designed to leverage the unique capabilities of quantum mechanics for enhanced computational efficiency. This section delves into the foundational principles of QNNs, their operational mechanics, and their potential advantages over classical neural networks.

Core Principles of QNNs

Quantum Bits (Qubits): Unlike classical bits that can only exist in a state of 0 or 1, qubits can exist in multiple states simultaneously due to superposition. This property allows QNNs to process vast amounts of information concurrently, enabling parallel computation that is unattainable by classical systems .
Entanglement: QNNs utilize quantum entanglement, where the state of one qubit is intrinsically linked to the state of another. This phenomenon facilitates complex correlations between data points, enhancing the network’s ability to learn intricate patterns from data.
Quantum Gates: The fundamental operations in QNNs are executed using quantum gates, which manipulate qubits similarly to how activation functions operate in classical neural networks. These gates enable the transformation and processing of quantum states through parameterized operations, described as: U(θ)=e−iθH where U(θ)is the quantum gate, θrepresents the parameters being optimized, and HH is the Hamiltonian operator governing the evolution

Hybrid Quantum-Classical Algorithms: Training QNNs often involves hybrid approaches that combine quantum and classical This integration optimizes quantum gate parameters using classical methods, such as gradient descent, which iteratively minimizes a cost function

C(θ): θ←θ−η∇C(θ)

where η is the learning rate .

Potential Advantages Over Classical Neural Networks

Quantum Neural Networks hold several advantages that may allow them to outperform classical neural networks in specific tasks:

Exponential Speedup: QNNs can potentially offer exponential improvements in processing speed for certain computational tasks, particularly those involving large-scale data or complex decision boundaries. The ability to explore multiple solutions simultaneously through superposition can lead to faster convergence during training.

Enhanced Pattern Recognition: The unique properties of quantum mechanics enable QNNs to excel in tasks requiring intricate pattern recognition. For instance, they can effectively classify quantum states or handle high-dimensional data structures more efficiently than classical models .

Improved Generalization: By exploiting quantum interference effects, QNNs may achieve better generalization capabilities on unseen data, reducing overfitting compared to their classical counterparts. This advantage stems from the inherent randomness and complexity introduced by quantum operations .

Handling Complex Data: QNNs are particularly well-suited for applications involving complex datasets, such as those found in quantum chemistry simulations or high-energy physics, where traditional neural networks might struggle due to their computational limitations.

Challenges and Future Directions

Despite their potential, the implementation of QNNs remains largely theoretical due to the current limitations of quantum hardware. As research progresses, efforts are focused on developing practical algorithms and architectures that can be realized on existing quantum devices. The ongoing exploration of QNNs could lead to significant breakthroughs in fields such as artificial intelligence, optimization problems, and beyond.

Real-World Applications of Quantum Machine Learning (QML)

Quantum machine learning (QML) is making significant strides in various real-world applications, leveraging the unique properties of quantum computing to enhance traditional machine learning tasks. Below are key areas where QML algorithms are applied:

1. Optimization Problems

● Finance: QML algorithms excel in optimizing complex financial processes like portfolio management and risk assessment. Quantum approaches, such as the Quantum Approximate Optimization Algorithm (QAOA), evaluate multiple investment strategies simultaneously, enabling efficient portfolio optimization that balances risk and return. The optimization objective function can be expressed as:

where w_i represents asset weights, x_i binary decision variables, C total investment capital, and λ is a penalty term .

● Logistics and Supply Chain Management: QML can solve combinatorial optimization problems like route planning using quantum-inspired algorithms such as Variational Quantum Eigensolver (VQE). This reduces transportation costs and maximizes efficiency by processing multiple configurations concurrently.

2. Pattern Recognition

● Image and Speech Recognition:

Quantum-enhanced Support Vector Machines (QSVMs) and quantum neural networks (QNNs) improve pattern recognition by efficiently processing large datasets. For instance, the kernel function used in QSVMs is:

Kij=∣⟨ϕ(xi)∣ϕ(xj)⟩∣

where ϕ(x) maps classical data to a quantum feature space, enabling better classification of images or speech .

● Anomaly Detection:

QML models excel at identifying outliers in high-dimensional data, benefiting applications like fraud detection. Quantum Principal Component Analysis (QPCA) efficiently identifies anomalies by capturing essential features while reducing computational overhead .

3. Data Clustering

● Customer Segmentation:

Quantum-enhanced clustering algorithms, such as quantum K-means, can efficiently segment customer data in high-dimensional feature spaces. These methods leverage quantum superposition to explore all cluster assignments simultaneously, minimizing the cost function:

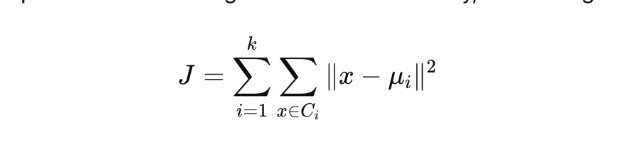
where C_i are clusters and μ_i their centroids .

● Dimensionality Reduction:

Quantum algorithms accelerate dimensionality reduction methods like PCA by solving eigenvalue problems exponentially faster, enhancing preprocessing steps in machine learning pipelines.

4. Drug Discovery and Material Science

● Molecular Simulations:

QML simulates molecular interactions with high accuracy using quantum chemistry algorithms like the Variational Quantum Solver (VQS). These simulations help researchers predict molecular properties and identify viable drug candidates efficiently .

● Material Optimization:

Quantum models predict material properties by solving quantum Hamiltonians. For example, the Schrödinger equation for material properties:

Hψ=Eψ

is efficiently solved using QML techniques, aiding in the design of materials with desired properties such as strength or conductivity.

5. Simulating Quantum Systems

Challenges and Limitations of Quantum Machine Learning (QML)

Quantum machine learning (QML) represents a promising frontier in computational intelligence, but its practical implementation faces significant hurdles. These challenges arise from hardware constraints, algorithmic complexity, integration difficulties, and theoretical limitations. Addressing these obstacles is essential for unlocking QML’s transformative potential.

1. Hardware Constraints

● Limited Qubit Availability:

Current quantum computers support only a limited number of qubits, restricting QML’s ability to tackle complex, high-dimensional problems. Many real-world applications require far more qubits than currently available, limiting scalability and practical use cases.

● Noisy Quantum Devices:

Quantum hardware is inherently prone to noise, causing errors during computation. Noise sources such as environmental interference can disrupt the fragile quantum states needed for QML. Error correction techniques, though essential, significantly increase computational overhead .

● Decoherence:

Qubits are susceptible to decoherence, the gradual loss of their quantum properties (e.g., superposition or entanglement) due to interactions with the environment. Decoherence often disrupts computations mid-process, leading to unreliable results.

● Specialized Infrastructure Requirements:

Operating quantum computers demands sophisticated infrastructure, including cryogenic cooling systems and advanced shielding against electromagnetic interference. These requirements escalate costs and complicate deployment .

2. Algorithmic Complexity

● Linear-Nonlinear Compatibility:

Quantum systems naturally operate linearly, but classical machine learning often relies on nonlinear activation functions for tasks like classification. Reconciling these differences remains an active area of research, as it limits the direct translation of classical models to quantum architectures .

● Barren Plateaus:

QNN training can suffer from barren plateaus, where gradients of the loss function vanish, making parameter optimization infeasible. This issue becomes more pronounced in high-dimensional quantum systems, requiring novel techniques to address.

● Data Encoding and Preparation:

Converting classical data into quantum states (quantum encoding) is computationally expensive, especially for large datasets. Efficient data preparation and encoding methods are critical for reducing overhead and improving algorithm performance .

2. Integration Challenges

● Hybrid Quantum-Classical Systems:

Most current QML implementations rely on hybrid systems, combining quantum and classical components. This approach often introduces latency, especially when data transfer between quantum processors and classical hardware is involved. Cloud-based quantum computing amplifies these issues due to network overhead.

● Standardization Issues:

The quantum computing landscape lacks standardization in software frameworks and protocols. Different platforms, such as IBM’s Qiskit and Google’s Cirq, vary significantly in design, hindering cross-compatibility and broader adoption .

4. Theoretical Limitations

● Understanding Quantum Algorithms:

The theoretical underpinnings of many quantum algorithms remain incomplete. This limited understanding complicates the development of efficient QML models and restricts their broader application .

● Measurement Sampling Requirements:

Quantum computations produce probabilistic outputs, requiring multiple measurements to obtain reliable results. This sampling process adds significant time overhead, especially in iterative algorithms like those used in machine learning.

Quantum Computing Platforms and Libraries for Quantum Machine Learning (QML)

Several quantum computing platforms and libraries are paving the way for the development and experimentation of quantum machine learning (QML) algorithms. These tools offer access to quantum hardware and simulators, along with software frameworks designed to facilitate QML research. Below are some prominent examples:

1. IBM Quantum Experience

Overview:

IBM Quantum Experience offers access to quantum computers and simulators via the cloud. Its open-source framework, Qiskit, allows developers to create and execute quantum algorithms, including those tailored for machine learning.

Key Features:

User-friendly interface for designing and visualizing quantum
Extensive documentation, tutorials, and community support for
Enables hybrid quantum-classical algorithm

2. Google Quantum AI

Overview:

Google Quantum AI provides advanced tools for quantum computing research, including TensorFlow Quantum (TFQ), which integrates seamlessly with the popular TensorFlow library.

Key Features:

Facilitates the creation of quantum machine learning models trained using classical machine learning methods.
Supports hybrid models combining quantum data processing with classical
Extensive API and integration support for flexible

3. D-Wave Systems

Overview:

D-Wave specializes in quantum annealing technology and provides cloud access to its quantum systems through its Ocean SDK.

Key Features:

Optimized for solving combinatorial optimization problems, such as training Boltzmann machines.
Ideal for applications requiring hybrid quantum-classical
Focused on efficiency for large-scale optimization tasks in industries like finance and logistics.

4. Rigetti Computing

Overview:

Rigetti offers the Forest platform, a cloud-based ecosystem for developing and running quantum algorithms using the Quil programming language.

Key Features:

Direct access to Rigetti’s quantum
Tools for integrating quantum algorithms with classical machine learning
Focus on streamlining QML development with real hardware and

5. Xanadu Quantum Technologies

Overview:

Xanadu leads in photonic quantum computing and offers the PennyLane library, designed for building and training quantum neural networks.

Key Features:

Combines quantum circuits with classical machine learning libraries such as PyTorch and TensorFlow.
Supports multiple backends, including simulators and hardware like Xanadu’s Borealis photonic processor.
Highly suitable for exploring quantum differentiable

6. Microsoft Quantum Development Kit

Overview:

Microsoft provides a comprehensive Quantum Development Kit (QDK) featuring the Q# programming language, which is tailored for quantum algorithm development.

Key Features:

Seamless integration with tools like Visual Studio and Jupyter
Libraries for QML, including quantum-enhanced data analysis and High-quality simulators for debugging and testing quantum algorithms before deployment on hardware.

Future Directions and Research Opportunities in Quantum Machine Learning (QML)