Meritshot Tutorials

  1. Home
  2. »
  3. Correlation and Covariance in R
SQL
R-Overview
Python

R Tutorial

Correlation and Covariance in R

Covariance and Correlation in R Programming

In R programming, covariance and correlation are used to measure the relationship between two

variables. Covariance measures the degree to which two variables change together, while correlation is a standardized measure of covariance that ranges from -1 to 1, indicating the strength and direction of the relationship.

Covariance in R Programming Language

In R, you can use the cov() function to calculate covariance between two variables. Here’s a basic

Example:

# Creating two vectors

x <- c(1, 2, 3, 4, 5)

y <- c(2, 4, 6, 8, 10)

# Calculating covariance between x and y

covariance <- cov(x, y)

print(covariance)

In this example, we create two vectors x and y, and then calculate their covariance using the cov() function. The result will be printed to the console.

If you have a dataset with multiple variables and want to calculate the covariance between all the variables, you can simply pass the entire dataset (in the form of a data frame) to the cov() function. Here’s an example using the built-in mtcars dataset:

# Load the built-in mtcars dataset

data(mtcars)

# Calculate the covariance matrix for the mtcars dataset

cov_matrix <- cov(mtcars)

print(cov_matrix)

In this example, we calculate the covariance matrix for all the variables in the mtcars dataset and print the resulting matrix to the console.

Correlation in R Programming Language

In R, you can use the cor() function to calculate the correlation between two variables. Here’s a basic

Example 2:

# Creating two vectors

x <- c(1, 2, 3, 4, 5)

y <- c(2, 4, 6, 8, 10)

# Calculating correlation between x and y

correlation <- cor(x, y)

print(correlation)

In this example, we create two vectors x and y, and then calculate their correlation using the cor() function. The result will be printed to the console.

If you have a dataset with multiple variables and want to calculate the correlation between all the variables, you can simply pass the entire dataset (in the form of a data frame) to the cor() function. Here’s an example using the built-in mtcars dataset:

# Load the built-in mtcars dataset

data(mtcars)

# Calculate the correlation matrix for the mtcars dataset

cor_matrix <- cor(mtcars)

print(cor_matrix)

In this example, we calculate the correlation matrix for all the variables in the mtcars dataset and print the resulting matrix to the console.

Keep in mind that the cor() function calculates the Pearson correlation coefficient by default. If you want to compute the Spearman or Kendall correlation coefficient, you can specify the method argument:

# Calculate the Spearman correlation coefficient

spearman_cor_matrix <- cor(mtcars, method = “spearman”)

print(spearman_cor_matrix)

# Calculate the Kendall correlation coefficient

kendall_cor_matrix <- cor(mtcars, method = “kendall”)

print(kendall_cor_matrix)

Covariance and Correlation in R

Now you know that to calculate covariance and correlation in R, you can use the built-in functions cov() and cor() respectively.

Here’s another example using two sample datasets, x and y:

# Create sample data

x <- c(1, 2, 3, 4, 5)

y <- c(2, 4, 6, 8, 10)

# Calculate covariance

covariance <- cov(x, y)

print(paste(“Covariance:”, covariance))

# Calculate correlation

correlation <- cor(x, y)

print(paste(“Correlation:”, correlation))

In this example, we create two sample datasets, x and y, and use the cov() and cor() functions to compute their covariance and correlation, respectively.

The output would be:

“Covariance: 5”

“Correlation: 1”

The covariance of 5 indicates that x and y change together, and the correlation of 1 indicates a perfect positive relationship between x and y.

Keep in mind that correlation coefficients are more interpretable than covariance values since

they’re standardized, while covariance values can be harder to interpret due to their dependence on the units of the variables.

Example 1: Perfect negative correlation

x1 <- c(1, 2, 3, 4, 5)

y1 <- c(5, 4, 3, 2, 1)

covariance1 <- cov(x1, y1)

correlation1 <- cor(x1, y1)

print(paste(“Covariance 1:”, covariance1))

print(paste(“Correlation 1:”, correlation1))

Output:

“Covariance 1: -2.5”

“Correlation 1: -1”

Example 2: Weak positive correlation

x2 <- c(1, 2, 3, 4, 5)

y2 <- c(3, 5, 6, 8, 10)

covariance2 <- cov(x2, y2)

correlation2 <- cor(x2, y2)

print(paste(“Covariance 2:”, covariance2))

print(paste(“Correlation 2:”, correlation2))

Output:

“Covariance 2: 4”

“Correlation 2: 0.8”

Example 3: No correlation

x3 <- c(1, 2, 3, 4, 5)

y3 <- c(5, 3, 2, 4, 1)

covariance3 <- cov(x3, y3)

correlation3 <- cor(x3, y3)

print(paste(“Covariance 3:”, covariance3))

print(paste(“Correlation 3:”, correlation3))

Output:

“Covariance 3: 0”

“Correlation 3: 0”

In these examples, we created datasets with different relationships between the variables: perfect negative correlation (Example 1), weak positive correlation (Example 2), and no correlation

(Example 3). The cov() and cor() functions help identify the nature of the relationship between the variables in each case.

Conversion of Covariance to Correlation in R

To convert a covariance matrix to a correlation matrix in R, you can use the following steps. We’ll use the cov2cor() function, which is part of the base R package.

1.  First, create a covariance matrix or use an existing one. For this example, let’s create a covariance matrix using the cov() function:

# Create a sample data frame

data <- data.frame(a = rnorm(10), b = rnorm(10), c = rnorm(10))

# Calculate the covariance matrix

cov_matrix <- cov(data)

print(cov_matrix)

2.  Now, use the cov2cor() function to convert the covariance matrix to a correlation matrix:

# Convert the covariance matrix to a correlation matrix

cor_matrix <- cov2cor(cov_matrix)

print(cor_matrix)

That’s it! The cor_matrix variable now contains the correlation matrix converted from the covariance matrix.

cor() function with an additional method parameter

In R, the cor() function can take an additional method parameter to specify the type of correlation coefficient to compute. There are three primary methods: “pearson” (default), “kendall”, and “spearman”. Here are examples of calculating correlation coefficients using these different methods:

Example 1: Perfect positive correlation with different methods

x <- c(1, 2, 3, 4, 5)

y <- c(2, 4, 6, 8, 10)

cor_pearson <- cor(x, y, method = “pearson”)

cor_kendall <- cor(x, y, method = “kendall”)

cor_spearman <- cor(x, y, method = “spearman”)

print(paste(“Pearson correlation:”, cor_pearson))

print(paste(“Kendall correlation:”, cor_kendall))

print(paste(“Spearman correlation:”, cor_spearman))

Output:

“Pearson correlation: 1”

“Kendall correlation: 1”

“Spearman correlation: 1”

Example 2: Weak negative correlation with different methods

x <- c(1, 2, 3, 4, 5)

y <- c(10, 8, 7, 5, 3)

cor_pearson <- cor(x, y, method = “pearson”)

cor_kendall <- cor(x, y, method = “kendall”)

cor_spearman <- cor(x, y, method = “spearman”)

print(paste(“Pearson correlation:”, cor_pearson))

print(paste(“Kendall correlation:”, cor_kendall))

print(paste(“Spearman correlation:”, cor_spearman))

Output:

“Pearson correlation: -0.898026511134676”

“Kendall correlation: -0.799999999999999”

“Spearman correlation: -0.999999999999999”

In these examples, we calculate the correlation coefficients using Pearson, Kendall, and Spearman methods. Pearson correlation is the default method and measures the linear relationship between variables, while Kendall and Spearman correlation coefficients are rank-based and measure the monotonic relationship between variables. The choice of method depends on the nature of the data and the desired analysis.

cov() function with an additional method parameter

cov(x, y, method) in R is a function that computes the covariance between two vectors x and y. The method parameter allows you to specify the method used to calculate the covariance.

# Example 1: Using the default method to calculate the covariance between two vectors x and y

x <- c(1, 2, 3, 4, 5)

y <- c(6, 7, 8, 9, 10)

cov(x, y)

# Example 2: Using the "pearson" method to calculate the Pearson correlation coefficient between two vectors x and y

x <- c(1, 2, 3, 4, 5)

y <- c(6, 7, 8, 9, 10)

cov(x, y, method = “pearson”)

# Example 3: Using the "kendall" method to calculate the Kendall rank correlation coefficient between two vectors x and y

x <- c(1, 2, 3, 4, 5)

y <- c(6, 7, 8, 9, 10)

cov(x, y, method = “kendall”)

# Example 4: Using the "spearman" method to calculate the Spearman rank correlation coefficient between two vectors x and y

x <- c(1, 2, 3, 4, 5)

y <- c(6, 7, 8, 9, 10)

cov(x, y, method = “spearman”)

Covariance Matrix

Covariance is the statistical measure that depicts the relationship between a pair of random variables that shows how the change in one variable causes changes in another variable. It is a measure of the degree to which two variables are linearly associated.

A covariance matrix is a square matrix that shows the covariance between different variables of a data frame. This helps us in understanding the relationship between different variables in a dataset.

To create a Covariance matrix from a data frame in the R Language, we use the cov() function. The cov() function forms the variance-covariance matrix. It takes the data frame as an argument and returns the covariance matrix as result.

Syntax:

cov( df )

Parameter:

  • df: determines the data frame for creating covariance

A positive value for the covariance matrix indicates that two variables tend to increase or decrease sequentially. A negative value for the covariance matrix indicates that as one variable increases, the second variable tends to decrease.

Example 1: Create Covariance matrix

R

# create sample data frame

sample_data <- data.frame( var1 = c(86, 82, 79, 83, 66),

var2 = c(85, 83, 80, 84, 65),

var3 = c(107, 127, 137, 117, 170))

# create covariance matrix

cov( sample_data )

Output:

var1

var2

var3

var1 60.7

63.9

-185.9

var2 63.9

68.3

-192.8

var3 -185.9

-192.8

585.8

Example 2: Create Covariance matrix

# create sample data frame

sample_data <- data.frame( var1 = rnorm(20,5,23),

                           var2 = rnorm(20,8,10))

# create covariance matrix

cov( sample_data )

Output:

var1        var2

var1 642.00590 -14.66349

var2 -14.66349      88.71560

Pearson Correlation Testing in R Programming

Correlation is a statistical measure that indicates how strongly two variables are related. It involves the relationship between multiple variables as well. For instance, if one is interested to know

whether there is a relationship between the heights of fathers and sons, a correlation coefficient can be calculated to answer this question. Generally, it lies between -1 and +1. It is a scaled version of covariance and provides the direction and strength of a relationship. Correlation coefficient test in R

Pearson Correlation Testing in R

There are mainly two types of correlation:

  1. Parametric Correlation – Pearson correlation(r): It measures a linear dependence between two variables (x and y) is known as a parametric correlation test because it depends on the distribution of the data.
  2. Non-Parametric Correlation – Kendall(tau) and Spearman(rho): They are rank-based correlation coefficients, and are known as non-parametric correlation.

Pearson Rank Correlation Coefficient Formula

Pearson Rank Correlation is a parametric correlation. The Pearson correlation coefficient is probably the most widely used measure for linear relationships between two normal distributed variables and thus often just called “correlation coefficient”. The formula for calculating the Pearson Rank

Correlation is as follows:

The Pearson Rank Correlation Coefficient, also known as Pearson’s r, measures the linear relationship between two variables. The formula is:

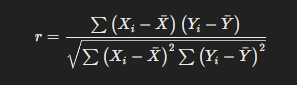
Where:

  • XiXi and YiYi are the individual data
  • XˉXˉ and YˉYˉ are the means of the XX and YY data sets,
  • rr is the Pearson correlation coefficient, ranging from -1 to 1:
    • r=1r=1 indicates a perfect positive linear
    • r=−1r=−1 indicates a perfect negative linear
    • r=0r=0 indicates no linear

This formula assesses how closely two sets of data points move together.

Note:

  • r takes a value between -1 (negative correlation) and 1 (positive correlation).
  • r = 0 means no
  • Can not be applied to ordinal
  • The sample size should be moderate (20-30) for good
  • Outliers can lead to misleading values means not robust with

Implementation in R

R Programming Language provides two methods to calculate the pearson correlation coefficient. By using the functions cor() or cor.test() it can be calculated. It can be noted that cor() computes the correlation coefficient whereas cor.test() computes the test for association or correlation between

paired samples. It returns both the correlation coefficient and the significance level(or p-value) of the correlation.

Syntax: cor(x, y, method = “pearson”) 
cor.test(x, y, method = “pearson”)

Parameters:

  • x, y: numeric vectors with the same length
  • method: correlation method

Correlation Coefficient Test In R Using cor() method

R

# R program to illustrate

# pearson Correlation Testing

# Using cor()

# Taking two numeric

# Vectors with same length

x = c(1, 2, 3, 4, 5, 6, 7)

y = c(1, 3, 6, 2, 7, 4, 5)

# Calculating

# Correlation coefficient

# Using cor() method

result = cor(x, y, method = “pearson”)

# Print the result

cat(“Pearson correlation coefficient is:”, result)

Output:

Pearson correlation coefficient is: 0.5357143

Correlation Coefficient Test In R Using cor.test() method

# R program to illustrate

# pearson Correlation Testing

# Using cor.test()

# Taking two numeric

# Vectors with same length

x = c(1, 2, 3, 4, 5, 6, 7)

y = c(1, 3, 6, 2, 7, 4, 5)

# Calculating

# Correlation coefficient

# Using cor.test() method

result = cor.test(x, y, method = “pearson”)

# Print the result

print(result)

Output:

Pearson’s product-moment correlation

data: x and y

t = 1.4186, df = 5, p-value = 0.2152

alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval:

-0.3643187 0.9183058

sample estimates: cor

0.5357143

In the output above:

  • T is the value of the test statistic (T = 4186)
  • p-value is the significance level of the test statistic (p-value = 2152).
  • alternative hypothesis is a character string describing the alternative hypothesis (true correlation is not equal to 0).
  • sample estimates is the correlation For Pearson correlation coefficient it’s named as cor (Cor.coeff = 0.5357).

Correlation Coefficient Test on External Dataset Data: Download the CSV file here.

# R program to illustrate

# Pearson Correlation Testing

# Import data into RStudio

df = read.csv(“Auto.csv”)

# Taking two column

# Vectors with same length

x = df$mpg

y = df$weight

# Calculating

# Correlation coefficient

# Using cor() method

result = cor(x, y, method = “pearson”)

# Print the result

cat(“Person correlation coefficient is:”, result)

# Using cor.test() method

res = cor.test(x, y, method = “pearson”)

print(res)

Output:

Person correlation coefficient is: -0.8782815 Pearson’s product-moment correlation

data: x and y

t = -31.709, df = 298, p-value < 2.2e-16

alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval:

-0.9018288 -0.8495329

sample estimates: cor

-0.8782815

Visualize Pearson Correlation Testing in R Programming

library(ggplot2)

# Scatter plot with correlation coefficient

ggplot(data = df, aes(x = weight, y = mpg)) +

  geom_point() +

  geom_smooth(method = “lm”, se = FALSE, color = “blue”) +

  annotate(“text”, x = mean(df$weight), y = max(df$mpg),

           label = paste(“Correlation =”, round(correlation, 2)),

           color = “red”, hjust = 0, vjust = 1) +

  labs(title = “Scatter Plot of MPG vs. Weight with Correlation Coefficient”,

       x = “Weight”, y = “MPG”) +

  theme_minimal()

Output:

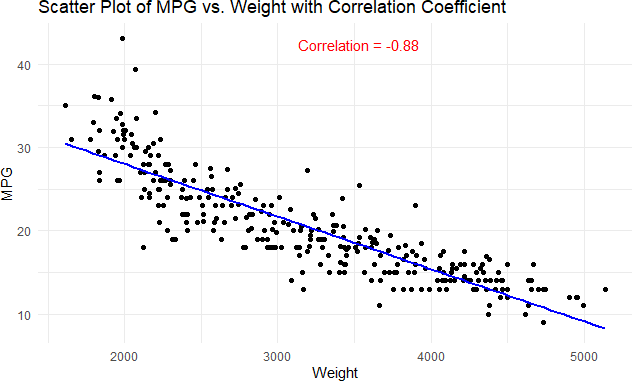
In this code, The geom_smooth() function with method = “lm” fits a linear model to the data. in the scatter plot calculated Pearson correlation coefficient. Adjust the position and appearance of the text as needed. The color of the annotation text is set to red for visibility. The resulting plot will give you both a visual representation of the relationship and the numeric correlation coefficient.

Spearman’s Rank Correlation Measure

In statistics, correlation Refers to the strength and direction of a relationship between two variables. The value of a correlation coefficient can range from -1 to 1, with the following interpretations:

  • -1: a perfect negative relationship between two variables
  • 0: no relationship between two variables
  • 1: a perfect positive relationship between two variables

One special type of correlation is called Spearman Rank Correlation, which is used to measure the correlation between two ranked variables. (e.g. rank of a student’s math exam score vs. rank of their science exam score in a class).

To calculate the Spearman rank correlation between two variables in R, we can use the following basic syntax:

corr <- cor.test(x, y, method = ‘spearman’)

The following examples show how to use this function in practice.

Example 1: Spearman Rank Correlation Between Vectors

The following code shows how to calculate the Spearman rank correlation between two vectors in R:

#define data

x <- c(70, 78, 90, 87, 84, 86, 91, 74, 83, 85)

y <- c(90, 94, 79, 86, 84, 83, 88, 92, 76, 75)

#calculate Spearman rank correlation between x and y

cor.test(x, y, method = ‘spearman’)

               Spearman’s rank correlation rho

data:  x and y

S = 234, p-value = 0.2324

alternative hypothesis: true rho is not equal to 0

sample estimates:

       rho

-0.4181818

From the output we can see that the Spearman rank correlation is -0.41818 and the corresponding p-value is 0.2324.

This indicates that there is a negative correlation between the two vectors.

However, since the p-value of the correlation is not less than 0.05, the correlation is not statistically significant.

Example 2: Spearman Rank Correlation Between Columns in Data Frame

The following code shows how to calculate the Spearman rank correlation between two column in a data frame:

#define data frame

df <- data.frame(team=c(‘A’, ‘B’, ‘C’, ‘D’, ‘E’, ‘F’, ‘G’, ‘H’, ‘I’, ‘J’),

                 points=c(67, 70, 75, 78, 73, 89, 84, 99, 90, 91),

                 assists=c(22, 27, 30, 23, 25, 31, 38, 35, 34, 32))

#calculate Spearman rank correlation between x and y

cor.test(df$points, df$assists, method = ‘spearman’)

               Spearman’s rank correlation rho

data:  df$points and df$assists

S = 36, p-value = 0.01165

alternative hypothesis: true rho is not equal to 0

sample estimates:

      rho

0.7818182

From the output we can see that the Spearman rank correlation is 0.7818 and the corresponding p- value is 0.01165.

This indicates that there is a strong positive correlation between the two vectors.

Since the p-value of the correlation is less than 0.05, the correlation is statistically significant.

Kendall Rank Correlation Measure

Kendall’s rank correlation provides a distribution free test of independence and a measure of the strength of dependence between two variables.

The Kendall Rank Correlation Coefficient, also known as Kendall’s Tau (τ), measures the ordinal association between two variables. In R, you can calculate Kendall’s Tau using the cor() function. Here’s how to do it:

Formula for Kendall’s Tau:

Kendall’s Tau is based on the number of concordant and discordant pairs in the data. The formula is:

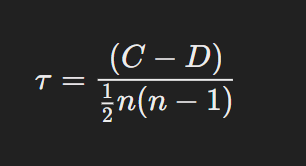
Where:

  • C is the number of concordant pairs (pairs where the ranks of both elements agree).
  • D is the number of discordant pairs (pairs where the ranks disagree).
  • n is the number of data

In R, you can calculate it as follows:

# Sample data

x <- c(1, 2, 3, 4, 5)

y <- c(5, 6, 7, 8, 7)

# Calculate Kendall’s Tau

tau <- cor(x, y, method = “kendall”)

# Display result

tau

Explanation:

  • x and y are the two numeric vectors for which you want to compute the
  • method = “kendall” specifies that the Kendall’s Tau correlation should be

This function returns a value between -1 and 1:

  • τ=1 τ=1 indicates a perfect positive
  • τ=−1 τ=−1 indicates a perfect negative
  • τ=0 τ=0 indicates no

Spearman’s rank correlation is satisfactory for testing a null hypothesis of independence between two variables but it is difficult to interpret when the null hypothesis is rejected. Kendall’s rank correlation improves upon this by reflecting the strength of the dependence between the variables being compared.

❮ Previous
Next ❯
ads website